Phân phối Poisson là một phân phối xác suất rời rạc, thường được sử dụng để mô tả số lần xảy ra của một sự kiện trong một khoảng thời gian cố định hoặc trong một không gian cố định, khi các sự kiện này xảy ra độc lập với nhau và với một tỷ lệ trung bình không đổi.
Các đặc điểm chính của phân phối Poisson:
- Tham số (λ – lambda): Đây là tỷ lệ trung bình của các sự kiện xảy ra trong một đơn vị thời gian hoặc không gian. λ còn được gọi là tham số Poisson và cũng là giá trị kỳ vọng (mean) của phân phối.
Hàm xác suất (PMF):
Hàm xác suất của phân phối Poisson được cho bởi:
trong đó:
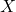là số lần xảy ra của sự kiện.
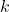là số lần cụ thể mà bạn muốn tính xác suất.
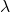là tỷ lệ trung bình của các sự kiện xảy ra trong một đơn vị thời gian hoặc không gian.
là cơ số của logarit tự nhiên (xấp xỉ 2.71828).
Kỳ vọng và phương sai:
- Kỳ vọng (mean):
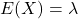
- Phương sai (variance):
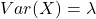
Ví dụ:
Giả sử một trung tâm dịch vụ khách hàng nhận trung bình 5 cuộc gọi mỗi giờ. Bạn muốn biết xác suất nhận được đúng 7 cuộc gọi trong một giờ. Trong trường hợp này:
- Tham số Poisson
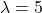
Xác suất để nhận được 7 cuộc gọi trong một giờ sẽ được tính bằng:
Ứng dụng:
Phân phối Poisson có nhiều ứng dụng trong các lĩnh vực khác nhau như:
- Dịch vụ khách hàng: Để dự đoán số lượng cuộc gọi hoặc yêu cầu dịch vụ trong một khoảng thời gian nhất định.
- Y học: Để mô hình hóa số lượng bệnh nhân đến khám tại một bệnh viện trong một khoảng thời gian.
- Bảo hiểm: Để tính toán số lượng yêu cầu bồi thường trong một khoảng thời gian.
- Giao thông: Để dự đoán số lượng xe hơi qua một điểm kiểm soát trong một khoảng thời gian.
Phân phối Poisson là một công cụ mạnh mẽ trong thống kê và xác suất, giúp mô hình hóa và giải quyết nhiều vấn đề