phân phối nhị thức - Truyện tranh khoa học

phân phối nhị thức là một loại phân phối xác suất rời rạc. Nó mô tả số lần thành công trong một loạt các thử nghiệm độc lập, mỗi thử nghiệm có hai kết quả có thể xảy ra: thành công hoặc thất bại. Phân phối nhị thức thường được sử dụng trong các tình huống mà kết quả của mỗi thử nghiệm chỉ có thể là một trong hai kết quả có thể xảy ra (ví dụ: đúng hoặc sai, có hoặc không).

Các đặc điểm chính của phân phối nhị thức:

Số lần thử (n): Số lần thử nghiệm được thực hiện.
Xác suất thành công (p): Xác suất thành công trong mỗi lần thử.
Xác suất thất bại (q): Xác suất thất bại trong mỗi lần thử, được tính bằng $q = 1 - p$ .

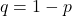Hàm xác suất (PMF):

Hàm xác suất của phân phối nhị thức được cho bởi:
$P(X = k) = \binom{n}{k} p^k (1 - p)^{n - k}$
trong đó:

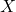$X$ là số lần thành công.
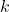$k$ là số lần thành công cần tính xác suất.
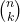$\binom{n}{k}$ là tổ hợp chập k của n.

Kỳ vọng và phương sai:

Kỳ vọng (mean): $E(X) = n \cdot p$
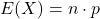
Phương sai (variance): $Var(X) = n \cdot p \cdot (1 - p)$

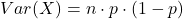
Ví dụ:

Giả sử bạn có một đồng xu cân đối và bạn ném đồng xu 10 lần. Bạn muốn biết xác suất để đồng xu ra mặt ngửa 6 lần. Trong trường hợp này:

Số lần thử nghiệm $n = 10$
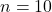
Xác suất thành công 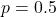$p = 0.5$ (đồng xu cân đối)
Xác suất thất bại $q = 0.5$

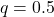
Xác suất để có được 6 lần mặt ngửa trong 10 lần ném sẽ được tính bằng:
$P(X = 6) = \binom{10}{6} (0.5)^6 (0.5)^4$

Ứng dụng:

Phân phối nhị thức có nhiều ứng dụng trong các lĩnh vực khác nhau như:

Thống kê: Để xác định xác suất của các sự kiện nhị thức.
Khoa học xã hội: Để mô hình hóa các khảo sát và thử nghiệm.
Y học: Để tính toán xác suất thành công của các phương pháp điều trị.

Phân phối nhị thức là một công cụ quan trọng trong thống kê và xác suất, giúp mô hình hóa và giải quyết nhiều vấn đề thực tế liên quan đến các thử nghiệm với hai kết quả có thể.

Các đặc điểm chính của phân phối nhị thức:

Hàm xác suất (PMF):

Kỳ vọng và phương sai:

Ví dụ:

Ứng dụng:

Related Posts

Để lại một bình luận Hủy