Phân phối đều

Phân phối đều (Uniform distribution) là một loại phân phối xác suất trong đó tất cả các giá trị trong một khoảng đều có xác suất xuất hiện bằng nhau. Có hai loại phân phối đều chính:

1. Phân phối đều rời rạc (Discrete Uniform Distribution):

Đây là phân phối mà các giá trị rời rạc có xác suất xuất hiện như nhau. Ví dụ điển hình là khi tung một con xúc xắc chuẩn, mỗi mặt (1, 2, 3, 4, 5, 6) có xác suất xuất hiện bằng nhau.

Nếu có n giá trị có thể xảy ra, xác suất của mỗi giá trị sẽ là:

2. Phân phối đều liên tục (Continuous Uniform Distribution):

Trong phân phối đều liên tục, các giá trị trong một khoảng liên tục đều có xác suất bằng nhau. Ví dụ, nếu bạn chọn ngẫu nhiên một số trong khoảng từ a đến b, mọi số trong khoảng đó có khả năng xuất hiện như nhau.

Hàm mật độ xác suất (PDF) của phân phối đều liên tục trên khoảng là:

Tính chất của phân phối đều:

• Trung bình của phân phối đều liên tục là:
  
• Phương sai là:
  

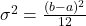
Ví dụ:

1. Phân phối đều rời rạc: Khi tung một đồng xu, xác suất xuất hiện mặt sấp hoặc mặt ngửa đều bằng .
2. Phân phối đều liên tục: Giả sử nhiệt độ mỗi ngày trong một mùa nào đó dao động từ 20°C đến 30°C và mỗi giá trị trong khoảng này có khả năng xuất hiện như nhau, thì đây là một ví dụ của phân phối đều liên tục trên khoảng .

Phân phối đều được sử dụng trong các bài toán liên quan đến ngẫu nhiên và xác suất mà mỗi kết quả có thể xảy ra với xác suất như nhau.