Phân phối chuẩn - Truyện tranh khoa học

bài hát ghi nhớ tính chất của phân phối chuẩn 1

bài hát giúp ghi nhớ tính chất của phân phối chuẩn 2

Phân phối chuẩn (hay còn gọi là phân phối Gauss hoặc phân phối Gaussian) là một trong những phân phối xác suất quan trọng và phổ biến nhất trong thống kê vì nhiều hiện tượng tự nhiên, xã hội tuân theo phân phối này, và nó cũng là cơ sở của nhiều phép thử thống kê.

Công thức hàm mật độ xác suất (PDF) của phân phối chuẩn cho một biến ngẫu nhiên $X$ với giá trị trung bình $\mu$ và độ lệch chuẩn $\sigma$ là:

$f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x - \mu)^2}{2\sigma^2}}$

Trong đó:

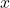$x$ là giá trị của biến ngẫu nhiên.
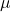$\mu$ là giá trị trung bình.
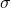$\sigma$ là độ lệch chuẩn.

Phân phối chuẩn có một hình dạng đặc trưng gọi là đường cong hình chuông (bell curve) giống như trong video, với các đặc điểm chính sau:

Đối xứng: Đường cong của phân phối chuẩn đối xứng qua giá trị trung bình, tức là nếu vẽ một đường thẳng từ đỉnh của đường cong dọc theo trục hoành (trục x), hai bên của đường cong sẽ hoàn toàn giống nhau.

Giá trị trung bình, trung vị và mode trùng nhau: Trong phân phối chuẩn, ba đại lượng thống kê quan trọng là giá trị trung bình (mean), trung vị (median), và mode đều trùng nhau và nằm tại điểm trung tâm của phân phối.

Đường cong hình chuông: Đường cong của phân phối chuẩn có hình chuông, với đỉnh tại giá trị trung bình, và giảm dần về hai phía.

Độ rộng của đường cong phụ thuộc vào độ lệch chuẩn: Độ lệch chuẩn (standard deviation) quyết định mức độ “phân tán” của dữ liệu. Độ lệch chuẩn càng lớn, đường cong càng rộng và thấp; độ lệch chuẩn càng nhỏ, đường cong càng hẹp và cao.

Phần lớn giá trị tập trung quanh trung bình: Khoảng 68% dữ liệu nằm trong khoảng ±1 lần độ lệch chuẩn tính từ giá trị trung bình, 95% dữ liệu nằm trong khoảng ±2 lần độ lệch chuẩn, và 99.7% nằm trong khoảng ±3 lần độ lệch chuẩn.

Related Posts

Để lại một bình luận Hủy