Phân phối Bernoulli là một phân phối xác suất rời rạc mô tả kết quả của một thí nghiệm chỉ có hai khả năng xảy ra: thành công (ký hiệu là 1) hoặc thất bại (ký hiệu là 0). Phân phối này được đặt theo tên nhà toán học Thụy Sĩ Jacob Bernoulli.
Đặc điểm của phân phối Bernoulli:
- Hai kết quả: Chỉ có hai kết quả có thể xảy ra:
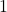 (thành công) hoặc
(thành công) hoặc 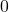 (thất bại).
(thất bại). - Xác suất:
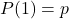 , trong đó
, trong đó 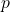 là xác suất thành công.
là xác suất thành công.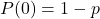 , trong đó
, trong đó  là xác suất thất bại.
là xác suất thất bại.![Rendered by QuickLaTeX.com p \in [0, 1]](https://ksmls.org/wp-content/ql-cache/quicklatex.com-9db8de53c5a66ee39d55ceccb68b267c_l3.png) :
: 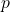 phải là một giá trị trong khoảng từ 0 đến 1.
phải là một giá trị trong khoảng từ 0 đến 1.
Hàm xác suất của phân phối Bernoulli:
Hàm xác suất ![]() của biến ngẫu nhiên Bernoulli
của biến ngẫu nhiên Bernoulli ![]() được định nghĩa như sau:
được định nghĩa như sau: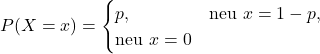
Trong đó ![]() là xác suất thành công.
là xác suất thành công.
Các tham số quan trọng:
- Kỳ vọng (giá trị trung bình):

Kỳ vọng của một phân phối Bernoulli là xác suất thành công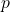 .
. - Phương sai:
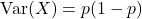
Phương sai đo lường mức độ phân tán của các giá trị quanh kỳ vọng.
Ví dụ về phân phối Bernoulli:
- Tung một đồng xu:
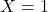 nếu là mặt sấp, và
nếu là mặt sấp, và 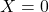 nếu là mặt ngửa.
nếu là mặt ngửa.- Nếu đồng xu là cân bằng, xác suất mặt sấp là
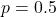 , và xác suất mặt ngửa là
, và xác suất mặt ngửa là 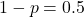 .
. - Trong một bài kiểm tra trắc nghiệm với một câu hỏi, nếu chọn ngẫu nhiên một đáp án,
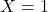 nếu trả lời đúng và
nếu trả lời đúng và 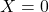 nếu trả lời sai.
nếu trả lời sai.
Ứng dụng:
Phân phối Bernoulli thường được sử dụng trong các thí nghiệm chỉ có hai kết quả, như trong thử nghiệm lâm sàng (kết quả điều trị thành công hoặc thất bại), hoặc kiểm tra sản phẩm đạt hay không đạt chất lượng.
Phân phối Bernoulli cũng là cơ sở để xây dựng các phân phối khác phức tạp hơn như phân phối nhị thức (binomial distribution), trong đó kết quả của nhiều thí nghiệm Bernoulli độc lập được cộng dồn.