Hồi quy tuyến tính đơn biến

Hồi quy tuyến tính đơn biến — “mô hình đoán đơn giản nhưng có gu” 😎 — chính là công cụ yêu thích của dân phân tích khi mới bước vào thế giới dự đoán. Nó giống như một anh chàng chỉ nhìn một yếu tố duy nhất để quyết định mọi thứ.

Ví dụ: muốn đoán giá nhà chỉ bằng diện tích — kiểu như “Nhà rộng thì chắc chắn đắt, khỏi cần nhìn nội thất hay vị trí!” 🏠💰

Mô hình này có dạng:
y = ax + b
Trong đó:

x là yếu tố duy nhất mà mô hình quan tâm (ví dụ: diện tích)
a là độ “sang chảnh” tăng giá theo diện tích (gọi là hệ số – coefficient)
b là mức giá khởi điểm kể cả nhà không có… đất (x=0)😅

Hồi quy tuyến tính đơn biến là một phương pháp thống kê để mô hình hóa mối quan hệ giữa một biến phụ thuộc (y) và một biến độc lập (x). Mục tiêu là tìm ra một đường thẳng (hoặc siêu phẳng trong không gian nhiều chiều) phù hợp nhất với dữ liệu, thường bằng cách giảm thiểu tổng bình phương sai số.

Công thức cơ bản

Hồi quy tuyến tính đơn giản (một biến độc lập):
$y = \beta_0 + \beta_1x + \epsilon$
Trong đó:

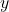$y$ : Biến phụ thuộc
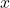$x$ : Biến độc lập
$\beta_0$ : Hệ số chặn (intercept)
$\beta_1$ : Hệ số góc (slope)
$\epsilon$ : Sai số ngẫu nhiên

Giả định chính

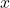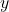Mối quan hệ giữa $x$ và $y$ là tuyến tính.
Sai số $\epsilon$ có giá trị trung bình bằng 0 và phương sai không đổi (homoscedasticity).
Các biến độc lập không có đa cộng tuyến (multicollinearity) nghiêm trọng.
Sai số có phân phối chuẩn (đặc biệt quan trọng trong kiểm định thống kê).

Phương pháp bình phương nhỏ nhất (Least Squares Method)

Phương pháp bình phương nhỏ nhất (Least Squares Method) là một kỹ thuật toán học được sử dụng để tìm ra đường thẳng hoặc mô hình tốt nhất phù hợp với một tập hợp dữ liệu bằng cách giảm thiểu tổng bình phương các sai số (khoảng cách giữa các điểm dữ liệu và mô hình dự đoán). Phương pháp này thường được sử dụng trong hồi quy tuyến tính.

Ý tưởng cơ bản

Cho một tập hợp dữ liệu gồm $n$ điểm $(x_i, y_i)$ , mục tiêu là tìm hàm $y = f(x)$ (thường là một đường thẳng $y = ax + b$ ) sao cho tổng bình phương sai số giữa giá trị thực tế $y_i$ và giá trị dự đoán $f(x_i)$ là nhỏ nhất:

$S = \sum_{i=1}^n (y_i - f(x_i))^2$

Trường hợp hồi quy tuyến tính đơn giản

Trong hồi quy tuyến tính đơn giản, mô hình là một đường thẳng $y = ax + b$ . Các tham số $a$ (độ dốc) và $b$ (hệ số chặn) được xác định bằng cách tối thiểu hóa hàm sai số:

$S = \sum_{i=1}^n (y_i - (ax_i + b))^2$

Để tìm $a$ và $b$ , ta lấy đạo hàm riêng của $S$ theo $a$ và $b$ , đặt chúng bằng 0, và giải hệ phương trình:

$\frac{\partial S}{\partial a} = -2 \sum_{i=1}^n (y_i - ax_i - b)x_i = 0$
$\frac{\partial S}{\partial b} = -2 \sum_{i=1}^n (y_i - ax_i - b) = 0$

Từ đó, ta có công thức:

$a = \frac{n \sum (x_i y_i) - \sum x_i \sum y_i}{n \sum x_i^2 - (\sum x_i)^2}$

$b = \frac{\sum y_i - a \sum x_i}{n}$

Trong đó:

$\sum x_i$ : Tổng các giá trị $x_i$
$\sum y_i$ : Tổng các giá trị $y_i$
$\sum x_i y_i$ : Tổng tích $x_i y_i$
$\sum x_i^2$ : Tổng bình phương $x_i$
$n$ : Số lượng điểm dữ liệu.

Ví dụ minh họa

Giả sử có các điểm dữ liệu: $(1, 2), (2, 4), (3, 5), (4, 4), (5, 5)$ . Ta muốn tìm đường thẳng $y = ax + b$ .

Tính các tổng:

$n = 5$
$\sum x_i = 1 + 2 + 3 + 4 + 5 = 15$
$\sum y_i = 2 + 4 + 5 + 4 + 5 = 20$
$\sum x_i y_i = 1 \cdot 2 + 2 \cdot 4 + 3 \cdot 5 + 4 \cdot 4 + 5 \cdot 5 = 2 + 8 + 15 + 16 + 25 = 66$
$\sum x_i^2 = 1^2 + 2^2 + 3^2 + 4^2 + 5^2 = 1 + 4 + 9 + 16 + 25 = 55$

Tính $a$ :
$a = \frac{5 \cdot 66 - 15 \cdot 20}{5 \cdot 55 - 15^2} = \frac{330 - 300}{275 - 225} = \frac{30}{50} = 0.6$
Tính $b$ :
$b = \frac{20 - 0.6 \cdot 15}{5} = \frac{20 - 9}{5} = \frac{11}{5} = 2.2$

Vậy, đường thẳng tốt nhất là: $y = 0.6x + 2.2$ .