hồi quy Ridge - Cùng Học Cùng Mơ

Hồi quy Ridge, anh bạn thân của Lasso, cũng là một “cao bồi” trong thế giới hồi quy, nhưng tính cách thì… hiền lành hơn một chút! Nếu Lasso là chàng cao bồi vung dây thừng chặt chém, đá bay các biến không quan trọng về 0, thì Ridge lại giống như một huấn luyện viên ôn hòa, không loại bỏ ai mà chỉ “dạy dỗ” các biến số để chúng bớt “quậy phá”.

Hồi quy Ridge (Ridge Regression) là một dạng hồi quy tuyến tính có thêm một “phạt L2” để kiểm soát độ phức tạp của mô hình. Thay vì loại bỏ biến như Lasso, Ridge làm cho các hệ số của các biến (những “con ngựa” trong mô hình) nhỏ đi, nhưng hiếm khi ép chúng về 0. Kết quả? Một mô hình vẫn giữ tất cả các biến nhưng với ảnh hưởng được “kiềm chế”, tránh việc mô hình quá “nhạy cảm” với dữ liệu.

Hãy tưởng tượng bạn đang quản lý một dàn nhạc giao hưởng, và mỗi nhạc công (biến số) đang chơi hết sức mình, nhưng đôi khi quá đà, làm bản nhạc (mô hình) rối tung. Hồi quy Ridge giống như một nhạc trưởng tài ba:

Thay vì đuổi nhạc công nào đó ra khỏi dàn nhạc (như Lasso), Ridge chỉ yêu cầu mọi người chơi nhỏ lại một chút (giảm hệ số).
Những nhạc công “hăng hái quá mức” (biến có hệ số lớn, dễ gây overfitting) sẽ bị Ridge “nhắc nhở” bằng cách giảm tầm ảnh hưởng của họ.
Kết quả? Bản nhạc vẫn đầy đủ các nhạc cụ (biến), nhưng hài hòa hơn, không bị lệch tông, tránh tình trạng “hát hò quá đà” (overfitting).

Công thức:

Trong hồi quy tuyến tính, ta tối thiểu hóa hàm mất mát:
$\text{Loss} = \sum (y_i - \hat{y}_i)^2$
(y_i là giá trị thực, $\hat{y}_i$ là giá trị dự đoán).

Ridge thêm một “phạt L2” vào:
$\text{Loss} = \sum (y_i - \hat{y}_i)^2 + \lambda \sum \beta_j^2$

$\beta_j$ : hệ số của các biến.
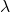$\lambda$ : mức độ phạt, càng lớn thì Ridge càng “nghiêm khắc”, ép các hệ số nhỏ lại.
Phần phạt $\sum \beta_j^2$ (bình phương hệ số) khiến các hệ số bị thu nhỏ nhưng hiếm khi bằng 0.

Ridge có gì vui?

Giữ hòa khí: Ridge không loại bỏ biến nào, cứ để mọi người trong dàn nhạc, chỉ cần “chơi nhỏ thôi” để tránh lấn át nhau.
Chống overfitting: Bằng cách giảm hệ số, Ridge giúp mô hình bớt “học vẹt” dữ liệu, dự đoán ổn định hơn trên dữ liệu mới.
Hài hước ở chỗ: Ridge giống như một ông thầy dịu dàng, không đuổi học sinh nào ra khỏi lớp, mà chỉ bảo: “Cả lớp trật tự, ai cũng quan trọng, nhưng đừng ai la to quá nhé!”

Khi nào dùng Ridge?

Khi bạn có nhiều biến và nghi ngờ chúng có thể liên quan lẫn nhau (đa cộng tuyến – multicollinearity).
Khi muốn giữ tất cả các biến trong mô hình nhưng cần giảm ảnh hưởng của những biến “hăng hái quá mức”.
Khi dữ liệu có nhiễu hoặc mô hình dễ bị overfitting.

Minh họa vui:

Giả sử bạn dự đoán giá nhà với các biến: diện tích, số phòng, số cột điện gần nhà, màu tường, v.v. Trong khi Lasso có thể thẳng tay “đuổi” màu tường và số cột điện (hệ số = 0), thì Ridge sẽ:

Giữ tất cả các biến, nhưng giảm hệ số của màu tường và số cột điện xuống rất nhỏ, kiểu: “Các bạn vẫn được ở lại, nhưng đừng làm ồn quá!”
Diện tích, số phòng vẫn có ảnh hưởng lớn, nhưng cũng được “kiềm chế” một chút để mô hình không quá lệ thuộc vào chúng.

So sánh với Lasso:

Lasso: Cao bồi mạnh mẽ, vung dây thừng (L1) chặt chém, loại bỏ biến không cần thiết. Kết quả: mô hình siêu gọn, chỉ giữ “ngôi sao”.
Ridge: Nhạc trưởng ôn hòa, dùng gậy chỉ huy (L2) để làm mọi người nhỏ giọng lại. Kết quả: mô hình đầy đủ, nhưng hài hòa hơn.
Kết hợp cả hai: Có cả Lasso và Ridge trong Elastic Net, như kiểu vừa có cao bồi vừa có nhạc trưởng, vừa loại bỏ biến thừa vừa làm mọi thứ cân bằng!

Kết luận:

Hồi quy Ridge là “nhạc trưởng” tài ba, giữ tất cả các biến trong mô hình nhưng làm cho chúng “hòa tấu” nhịp nhàng hơn bằng cách giảm hệ số. Nó giúp mô hình ổn định, tránh overfitting, đặc biệt khi các biến có liên quan chặt chẽ. So với Lasso, Ridge hiền hơn, không “đuổi” ai, nhưng vẫn đảm bảo bữa tiệc dữ liệu không bị hỗn loạn! 🎶